【算法】栈与队列

基础

队列是先进先出，栈是先进后出。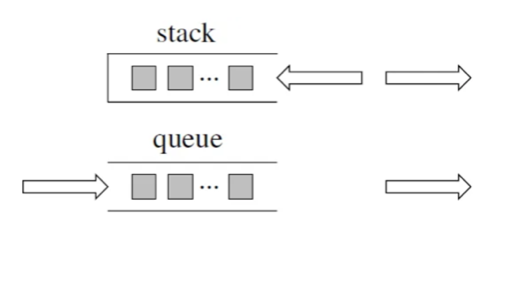

在Java中，栈（Stack）和队列（Queue）也是非常重要的数据结构，它们在Java集合框架中有着各自的实现和应用。让我们深入了解一下Java中的栈和队列的实现及其特点。

Java中的栈（Stack）

Java中的Stack类实现了一个后进先出（LIFO）的数据结构。它继承自Vector，提供了允许数据从栈顶添加和移除的方法。然而，由于Stack类是基于Vector实现的，这导致它在多线程环境下并不安全，且性能不是最优的。因此，推荐使用更现代的数据结构，如Deque接口。

主要方法：

• push(E item): 将元素添加到栈顶。
• pop(): 移除栈顶元素并返回该元素。
• peek(): 返回栈顶元素但不移除。
• empty(): 检查栈是否为空。
• search(Object o): 返回对象在栈中的位置，以1为基底。

Java中的队列（Queue）

在Java中，Queue接口定义了队列的基本操作。队列通常是先进先出（FIFO）的，但特定类型的队列如优先队列（PriorityQueue）则根据元素的自然顺序或比较器来决定元素的出队顺序。

实现类：

• LinkedList: 实现了Queue接口，提供了标准的队列操作。它允许元素为null。
• PriorityQueue: 一个基于优先堆的无界队列，元素根据其自然顺序或比较器进行排序。
• ArrayDeque: 如果你不需要线程安全性，ArrayDeque是比LinkedList更高效的双端队列（Deque）实现。

主要方法：

• add(E e): 将元素添加到队列尾部。如果成功，返回true；如果没有空间，则抛出IllegalStateException。
• offer(E e): 将元素添加到队列尾部，如果队列已满，则返回false。
• remove(): 移除队列头的元素。如果队列为空，则抛出NoSuchElementException。
• poll(): 移除并返回队列头部的元素。如果队列为空，则返回null。
• element(): 返回队列头部的元素但不移除。如果队列为空，则抛出NoSuchElementException。
• peek(): 返回队列头部的元素但不移除。如果队列为空，则返回null。

推荐使用
对于多数需要使用栈的场景，Java官方推荐使用ArrayDeque。它比Stack类更快，因为ArrayDeque是循环数组的形式实现的，这使得它在不涉及线程安全的环境中具有更高的性能。同样的，对于队列操作，ArrayDeque也是一个优良的选择，尤其是当你需要一个同时支持栈和队列操作的高效数据结构时。

232.用栈实现队列

请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作（push、pop、peek、empty）：

实现 MyQueue 类：
void push(int x) 将元素 x 推到队列的末尾
int pop() 从队列的开头移除并返回元素
int peek() 返回队列开头的元素
boolean empty() 如果队列为空，返回 true ；否则，返回 false

说明：
你 只能 使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
你所使用的语言也许不支持栈。你可以使用 list 或者 deque（双端队列）来模拟一个栈，只要是标准的栈操作即可。

示例：

MyQueue queue = new MyQueue();
queue.push(1);
queue.push(2);
queue.peek();  // 返回 1
queue.pop();   // 返回 1
queue.empty(); // 返回 false

使用栈来模拟队列的行为，如果仅仅用一个栈，是一定不行的，所以需要两个栈一个输入栈，一个输出栈，这里要注意输入栈和输出栈的关系。
在push数据的时候，只要数据放进输入栈就好，但在pop的时候，操作就复杂一些，输出栈如果为空，就把进栈数据全部导入进来（注意是全部导入），再从出栈弹出数据，如果输出栈不为空，则直接从出栈弹出数据就可以了。
最后如何判断队列为空呢？如果进栈和出栈都为空的话，说明模拟的队列为空了。
在代码实现的时候，会发现pop() 和 peek()两个函数功能类似，代码实现上也是类似的，可以思考一下如何把代码抽象一下。

class MyQueue {

    Stack<Integer> stackIn;
    Stack<Integer> stackOut;

    public MyQueue() {
        stackIn = new Stack<>(); // 负责进栈
        stackOut = new Stack<>(); // 负责出栈
    }
    
    public void push(int x) {
        stackIn.push(x);
    }
    
    public int pop() {
        dumpstackIn();
        return stackOut.pop();
    }
    
    public int peek() {
        dumpstackIn();
        return stackOut.peek();
    }
    
    public boolean empty() {
        return stackIn.isEmpty() && stackOut.isEmpty();
    }
    // 如果stackOut为空，那么将stackIn中的元素全部放到stackOut中
    private void dumpstackIn(){
        if(!stackOut.isEmpty()) return;
        while(!stackIn.isEmpty()){
            stackOut.push(stackIn.pop());
        }
    }
}

225. 用队列实现栈

请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）。

实现 MyStack 类：
void push(int x) 将元素 x 压入栈顶。
int pop() 移除并返回栈顶元素。
int top() 返回栈顶元素。
boolean empty() 如果栈是空的，返回 true ；否则，返回 false 。

注意：
你只能使用队列的标准操作 —— 也就是 push to back、peek/pop from front、size 和 is empty 这些操作。
你所使用的语言也许不支持队列。 你可以使用 list （列表）或者 deque（双端队列）来模拟一个队列 , 只要是标准的队列操作即可。

题解

队列模拟栈，其实一个队列就够了，一个队列在模拟栈弹出元素的时候只要将队列头部的元素（除了最后一个元素外） 重新添加到队列尾部，此时再去弹出元素就是栈的顺序了。
但题目要求两个队列模拟，队列是先进先出的规则，把一个队列中的数据导入另一个队列中，数据的顺序并没有变，并没有变成先进后出的顺序。
所以用栈实现队列， 和用队列实现栈的思路还是不一样的，这取决于这两个数据结构的性质。
但是依然还是要用两个队列来模拟栈，只不过没有输入和输出的关系，而是另一个队列完全用来备份的！

class MyStack {
    Queue<Integer> queue1;
    Queue<Integer> queue2;

    public MyStack() {
        queue1 = new LinkedList<>();
        queue2 = new LinkedList<>();
    }
    
    public void push(int x) {
        queue2.offer(x); // 先放在辅助队列中
        while(!queue1.isEmpty()){
            queue2.offer(queue1.poll());
        }
        Queue<Integer> queueTemp;
        queueTemp = queue1;
        queue1 = queue2;
        queue2 = queueTemp;
    }
    
    public int pop() {
        return queue1.poll();
    }
    
    public int top() {
        return queue1.peek();
    }
    
    public boolean empty() {
        return queue1.isEmpty();
    }
}

20. 有效的括号

给定一个只包括 ‘(‘，’)’，’{‘，’}’，’[‘，’]’ 的字符串 s ，判断字符串是否有效。

有效字符串需满足：
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
每个右括号都有一个对应的相同类型的左括号。

class Solution {
    public boolean isValid(String s) {
        Deque<Character> deque = new LinkedList<>(); // Deque 用双端队列解决 Queue 是java中的普通队列
        char ch;
        for(int i = 0; i < s.length(); i++){
            ch = s.charAt(i);
            if(ch == '('){
                deque.push(')');
            }else if(ch == '{'){
                deque.push('}');
            }else if(ch == '['){
                deque.push(']');
            } else if (deque.isEmpty() || deque.peek() != ch){
                return false;
            }else{
                deque.pop();
            }
        }
        return deque.isEmpty();
    }
}

1047. 删除字符串中的所有相邻重复项

给出由小写字母组成的字符串 s，重复项删除操作会选择两个相邻且相同的字母，并删除它们。
在 s 上反复执行重复项删除操作，直到无法继续删除。
在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。

输入：”abbaca”
输出：”ca”
解释：
例如，在 “abbaca” 中，我们可以删除 “bb” 由于两字母相邻且相同，这是此时唯一可以执行删除操作的重复项。之后我们得到字符串 “aaca”，其中又只有 “aa” 可以执行重复项删除操作，所以最后的字符串为 “ca”。

class Solution {
    public String removeDuplicates(String s) {
        //ArrayDeque会比LinkedList在除了删除元素这一点外会快一点
        //参考：https://stackoverflow.com/questions/6163166/why-is-arraydeque-better-than-linkedlist
        ArrayDeque<Character> deque = new ArrayDeque<>();
        char ch;
        for(int i = 0; i < s.length(); i++){
            ch = s.charAt(i);
            if(deque.isEmpty() || deque.peek() != ch){
                deque.push(ch);
            }else{
                deque.pop();
            }
        }
        String str = "";
        while(!deque.isEmpty()){
            str = deque.pop() + str;
        }
        return str;
    }
}

150. 逆波兰表达式求值

给你一个字符串数组 tokens ，表示一个根据 逆波兰表示法 表示的算术表达式。
请你计算该表达式。返回一个表示表达式值的整数。

注意：
有效的算符为 ‘+’、’-‘、’*’ 和 ‘/‘ 。
每个操作数（运算对象）都可以是一个整数或者另一个表达式。
两个整数之间的除法总是 向零截断 。
表达式中不含除零运算。
输入是一个根据逆波兰表示法表示的算术表达式。
答案及所有中间计算结果可以用 32 位 整数表示。

示例 1：
输入：tokens = [“2”,”1”,”+”,”3”,”*”]
输出：9
解释：该算式转化为常见的中缀算术表达式为：((2 + 1) * 3) = 9
示例 2：

输入：tokens = [“4”,”13”,”5”,”/“,”+”]
输出：6
解释：该算式转化为常见的中缀算术表达式为：(4 + (13 / 5)) = 6
示例 3：

输入：tokens = [“10”,”6”,”9”,”3”,”+”,”-11”,”“,”/“,”“,”17”,”+”,”5”,”+”]
输出：22
解释：该算式转化为常见的中缀算术表达式为：
((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22

题解

其实逆波兰表达式相当于是二叉树中的后序遍历。 大家可以把运算符作为中间节点，按照后序遍历的规则画出一个二叉树。但我们没有必要从二叉树的角度去解决这个问题，只要知道逆波兰表达式是用后序遍历的方式把二叉树序列化了，就可以了。
进一步看，本题中每一个子表达式要得出一个结果，然后拿这个结果再进行运算，那么这岂不就是一个相邻字符串消除的过程，和1047.删除字符串中的所有相邻重复项 (opens new window)中的对对碰游戏是不是就非常像了。

我们习惯看到的表达式都是中缀表达式，因为符合我们的习惯，但是中缀表达式对于计算机来说就不是很友好了。
例如：4 + 13 / 5，这就是中缀表达式，计算机从左到右去扫描的话，扫到13，还要判断13后面是什么运算符，还要比较一下优先级，然后13还和后面的5做运算，做完运算之后，还要向前回退到 4 的位置，继续做加法，你说麻不麻烦！
那么将中缀表达式，转化为后缀表达式之后：[“4”, “13”, “5”, “/“, “+”] ，就不一样了，计算机可以利用栈来顺序处理，不需要考虑优先级了。也不用回退了， 所以后缀表达式对计算机来说是非常友好的。

class Solution {
    public int evalRPN(String[] tokens) {
        Deque<Integer> stack = new LinkedList();
        for(String s : tokens){
            if("+".equals(s)){// leetcode 内置jdk的问题，不能使用==判断字符串是否相等
                stack.push(stack.pop() + stack.pop());
            }else if("-".equals(s)){
                stack.push(-stack.pop() + stack.pop());
            }else if("/".equals(s)){
                int temp1 = stack.pop(); 
                int temp2 = stack.pop();
                stack.push(temp2 / temp1);
            }else if("*".equals(s)){
                stack.push(stack.pop() * stack.pop());
            }else{
                stack.push(Integer.valueOf(s));
            }
        }
        return stack.pop();
    }
}

在 Java 中使用 Deque（双端队列）代替传统的 Stack 类来实现堆栈操作（如在解析逆波兰表达式的例子中所示）有几个原因：

1. 性能更优：Java 官方文档推荐使用 ArrayDeque 作为栈，因为相比于 Stack 类，ArrayDeque 有更好的性能。Stack 继承自 Vector，后者是一个同步的集合类，因此每个操作都涉及锁定和解锁，这在多数情况下会导致不必要的性能开销。而 ArrayDeque 则没有这些额外的开销，因为它不是线程安全的。
2. 更加现代和灵活：Stack 类是早期 Java 版本中的一个遗留类，而 Deque 接口及其实现类（如 LinkedList 和 ArrayDeque）则是 Java 集合框架的一部分，提供了更多的功能和灵活性。例如，Deque 支持在两端插入和移除元素，使其不仅可以作为栈使用，还可以作为队列使用。
3. 更好的接口设计：Deque 接口提供了一组更为一致和完整的方法来操作数据，这使得代码更容易理解和维护。例如，使用 push、pop 和 peek 方法来模拟传统的栈操作。

239. 滑动窗口最大值

给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回 滑动窗口中的最大值 。

示例 1：
输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]
解释：
滑动窗口的位置 最大值

---

[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7

示例 2：
输入：nums = [1], k = 1
输出：[1]

题解

有的同学可能会想用一个大顶堆（优先级队列）来存放这个窗口里的k个数字，这样就可以知道最大的最大值是多少了， 但是问题是这个窗口是移动的，而大顶堆每次只能弹出最大值，我们无法移除其他数值，这样就造成大顶堆维护的不是滑动窗口里面的数值了。所以不能用大顶堆。
这道题正确的思路是应用单调队列解决，队列没有必要维护窗口里的所有元素，只需要维护有可能成为窗口里最大值的元素就可以了，同时保证队列里的元素数值是由大到小的。
对于窗口里的元素{2, 3, 5, 1 ,4}，单调队列里只维护{5, 4} 就够了，保持单调队列里单调递减，此时队列出口元素就是窗口里最大元素。

此时大家应该怀疑单调队列里维护着{5, 4} 怎么配合窗口进行滑动呢？设计单调队列的时候，pop，和push操作要保持如下规则：

1. pop(value)：如果窗口移除的元素value等于单调队列的出口元素，那么队列弹出元素，否则不用任何操作
2. push(value)：如果push的元素value大于入口元素的数值，那么就将队列入口的元素弹出，直到push元素的数值小于等于队列入口元素的数值为止

// 解法一，自定义数组
class MyQueue{
    Deque<Integer> deque = new LinkedList<>();
    // 弹出元素时，比较弹出的数值是否等于队列出口的数值，如果相等则弹出
        // 同时判断队列当前是否为空
    void poll(int val){
        if(!deque.isEmpty() && val == deque.peek()){
            deque.poll();
        }
    }

    //添加元素时，如果要添加的元素大于入口处的元素，就将入口元素弹出
    //保证队列元素单调递减
    //比如此时队列元素3,1，2将要入队，比1大，所以1弹出，此时队列：3,2
    void add(int val){
        while(!deque.isEmpty() && val > deque.getLast()){
            deque.removeLast();
        }
        deque.add(val);
    }
    //队列队顶元素始终为最大值
    int peek(){
        return deque.peek();
    }
}

class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        if(nums.length == 1){
            return nums;
        }
        int len = nums.length - k + 1;
        // 存放结果元素的数组
        int[] res = new int[len];
        int num = 0;
        // 自定义队列
        MyQueue myQueue = new MyQueue();
        // 先将前k元素放入队列
        for(int i = 0; i < k; i++){
            myQueue.add(nums[i]);
        }
        res[num++] = myQueue.peek();
        for(int i = k; i < nums.length; i++){
            // 滑动窗口移除最前面的元素，移除时判断该元素是否放入队列
            myQueue.poll(nums[i - k]);
            // 滑动窗口加入最后面的元素
            myQueue.add(nums[i]);
            // 记录最大值
            res[num++] = myQueue.peek();
        }
        return res;
    }
}


// 解法二，利用双端队列手动实现单调队列
/**
 * 用一个单调队列来存储对应的下标，每当窗口滑动的时候，直接取队列的头部指针对应的值放入结果集即可
 * 单调队列类似 （tail -->） 3 --> 2 --> 1 --> 0 (--> head) (右边为头结点，元素存的是下标)
 */
class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        ArrayDeque<Integer> deque = new ArrayDeque<>();
        int n = nums.length;
        int[] res = new int[n - k + 1];
        int idx = 0;
        for(int i = 0; i < n; i++){
            // 根据题意，i为nums下标，是要在[i - k + 1, i] 中选到最大值，只需要保证两点
            // 1.队列头结点需要在[i - k + 1, i]范围内，不符合则要弹出
            while(!deque.isEmpty() && deque.peek() < i - k + 1){
                deque.poll();
            }
            // 2.既然时单调，就要保证每次放进去的数字都要比末尾的大，否则也弹出
            while(!deque.isEmpty() && nums[deque.peekLast()] < nums[i]){
                deque.pollLast();
            }
            deque.offer(i);
            // 因为单调，当i增长到符合第一个k范围的时候，每滑动一步都将队列头节点放入结果就行了
            if(i >= k - 1){
                res[idx++] = nums[deque.peek()];
            }
        }
        return res;
    }
}

347.前 K 个高频元素

给定一个非空的整数数组，返回其中出现频率前 k 高的元素。

示例 1:
输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]

示例 2:
输入: nums = [1], k = 1
输出: [1]

提示：
你可以假设给定的 k 总是合理的，且 1 ≤ k ≤ 数组中不相同的元素的个数。
你的算法的时间复杂度必须优于 $O(n \log n)$ , n 是数组的大小。
题目数据保证答案唯一，换句话说，数组中前 k 个高频元素的集合是唯一的。
你可以按任意顺序返回答案。

题解

首先统计元素出现的频率，这一类的问题可以使用map来进行统计。

然后是对频率进行排序，这里我们可以使用一种 容器适配器就是优先级队列。

什么是优先级队列呢？
其实就是一个披着队列外衣的堆，因为优先级队列对外接口只是从队头取元素，从队尾添加元素，再无其他取元素的方式，看起来就是一个队列。
而且优先级队列内部元素是自动依照元素的权值排列。那么它是如何有序排列的呢？
缺省情况下priority_queue利用max-heap（大顶堆）完成对元素的排序，这个大顶堆是以vector为表现形式的complete binary tree（完全二叉树）。

什么是堆呢？
堆是一棵完全二叉树，树中每个结点的值都不小于（或不大于）其左右孩子的值。 如果父亲结点是大于等于左右孩子就是大顶堆，小于等于左右孩子就是小顶堆。
所以大家经常说的大顶堆（堆头是最大元素），小顶堆（堆头是最小元素），如果懒得自己实现的话，就直接用priority_queue（优先级队列）就可以了，底层实现都是一样的，从小到大排就是小顶堆，从大到小排就是大顶堆。

本题我们就要使用优先级队列来对部分频率进行排序。
为什么不用快排呢， 使用快排要将map转换为vector的结构，然后对整个数组进行排序， 而这种场景下，我们其实只需要维护k个有序的序列就可以了，所以使用优先级队列是最优的。

此时要思考一下，是使用小顶堆呢，还是大顶堆？
有的同学一想，题目要求前 K 个高频元素，那么果断用大顶堆啊。
那么问题来了，定义一个大小为k的大顶堆，在每次移动更新大顶堆的时候，每次弹出都把最大的元素弹出去了，那么怎么保留下来前K个高频元素呢。
而且使用大顶堆就要把所有元素都进行排序，那能不能只排序k个元素呢？
所以我们要用小顶堆，因为要统计最大前k个元素，只有小顶堆每次将最小的元素弹出，最后小顶堆里积累的才是前k个最大元素。

// 大顶堆解法
class Solution {
    public int[] topKFrequent(int[] nums, int k) {
        Map<Integer, Integer> map = new HashMap<>();
        for(int num : nums){
            map.put(num, map.getOrDefault(num, 0) + 1);
        }
        //在优先队列中存储二元组(num, cnt),cnt表示元素值num在数组中的出现次数
        //出现次数按从队头到队尾的顺序是从大到小排,出现次数最多的在队头(相当于大顶堆)
        PriorityQueue<int[]> pq = new PriorityQueue<>((pair1, pair2) -> pair2[1] - pair1[1]);
        for(Map.Entry<Integer, Integer> entry : map.entrySet()){// 大顶堆需要对所有元素进行排序
            pq.add(new int[]{entry.getKey(), entry.getValue()});
        }
        int[] ans = new int[k];
        for(int i = 0; i < k; i++){ //依次从队头弹出k个就是频率前k高的
            ans[i] = pq.poll()[0];
        }
        return ans;
    }
}

// 小顶堆解法
class Solution {
    public int[] topKFrequent(int[] nums, int k) {
        Map<Integer, Integer> map = new HashMap<>();
        for(int num : nums){
            map.put(num, map.getOrDefault(num, 0) + 1);
        }
        //在优先队列中存储二元组(num, cnt),cnt表示元素值num在数组中的出现次数
        //出现次数按从队头到队尾的顺序是从大到小排,出现次数最多的在队头(相当于大顶堆)
        PriorityQueue<int[]> pq = new PriorityQueue<>((pair1, pair2) -> pair1[1] - pair2[1]);
        for(Map.Entry<Integer, Integer> entry : map.entrySet()){//小顶堆只需要维持k个
            if(pq.size() < k){
                pq.add(new int[]{entry.getKey(), entry.getValue()});
            }else{
                if(entry.getValue() > pq.peek()[1]){ //当前元素出现次数大于小顶堆的根结点(这k个元素中出现次数最少的那个)
                    pq.poll(); //弹出队头(小顶堆的根结点),即把堆里出现次数最少的那个删除,留下的就是出现次数多的了
                    pq.add(new int[]{entry.getKey, entry.getValue});
                }
            }
        }
        int[] ans = new int[k];
        for(int i = k-1; i >= 0; i--){ //依次弹出小顶堆,先弹出的是堆的根,出现次数少,后面弹出的出现次数多
            ans[i] = pq.poll()[0];
        }
        return ans;
    }
}

总结

栈里面的元素在内存中是连续分布的么？

这个问题有两个陷阱：
陷阱1：栈是容器适配器，底层容器使用不同的容器，导致栈内数据在内存中不一定是连续分布的。
陷阱2：缺省情况下，默认底层容器是deque，那么deque在内存中的数据分布是什么样的呢？ 答案是：不连续的，下文也会提到deque。

一个队列在模拟栈弹出元素的时候只要将队列头部的元素（除了最后一个元素外） 重新添加到队列尾部，此时在去弹出元素就是栈的顺序了。

栈在系统中的应用

如果还记得编译原理的话，编译器在词法分析的过程中处理括号、花括号等这个符号的逻辑，就是使用了栈这种数据结构。

再举个例子，linux系统中，cd这个进入目录的命令我们应该再熟悉不过了。cd a/b/c/../../
这个命令最后进入a目录，系统是如何知道进入了a目录呢 ，这就是栈的应用。

递归的实现是栈：每一次递归调用都会把函数的局部变量、参数值和返回地址等压入调用栈中，然后递归返回的时候，从栈顶弹出上一次递归的各项参数，所以这就是递归为什么可以返回上一层位置的原因。