344.反转字符串 编写一个函数,其作用是将输入的字符串反转过来。输入字符串以字符数组 s 的形式给出。
示例 1:
示例 2:
使用双指针解决这个问题,同时可以用异或来交换数值
1 2 3 4 5 6 7 8 9 10 11 12 13 class Solution { public void reverseString (char [] s) { int l = 0 ; int r = s.length - 1 ; while (l < r){ s[l] ^= s[r]; s[r] ^= s[l]; s[l] ^= s[r]; l++; r--; } } }
541. 反转字符串II 给定一个字符串 s 和一个整数 k,从字符串开头算起, 每计数至 2k 个字符,就反转这 2k 个字符中的前 k 个字符。
如果剩余字符小于 2k 但大于或等于 k 个,则反转前 k 个字符,其余字符保持原样。
示例:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 class Solution { public String reverseStr (String s, int k) { StringBuffer res = new StringBuffer (); int length = s.length(); int start = 0 ; while (start < length){ StringBuffer temp = new StringBuffer (); int firstK = (start + k > length) ? length : start + k; int secondK = (start + (2 *k) > length) ? length : start + (2 *k); temp.append(s.substring(start, firstK)); res.append(temp.reverse()); if (firstK < secondK){ res.append(s.substring(firstK, secondK)); } start += (2 *k); } return res.toString(); } } class Solution { public String reverseStr (String s, int k) { char [] ch = s.toCharArray(); for (int i = 0 ; i < ch.length; i+=2 *k){ int start = i; int end = Math.min(ch.length-1 ,start+k-1 ); while (start < end){ ch[start] ^= ch[end]; ch[end] ^= ch[start]; ch[start] ^= ch[end]; start++; end--; } } return new String (ch); } }
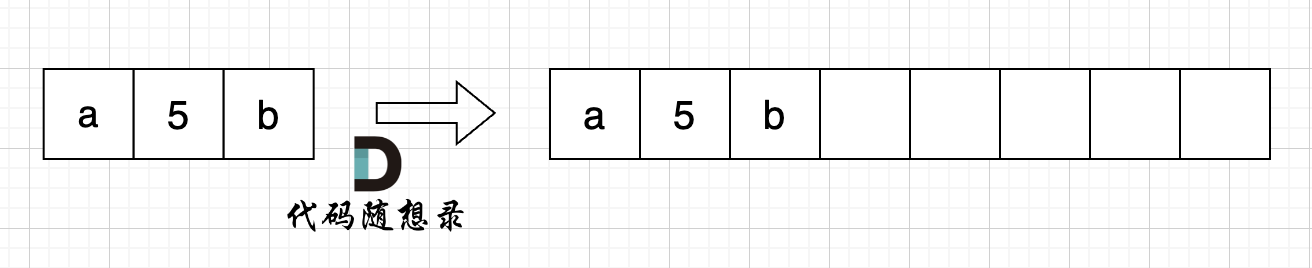
替换数字 给定一个字符串 s,它包含小写字母和数字字符,请编写一个函数,将字符串中的字母字符保持不变,而将每个数字字符替换为number。
如果想把这道题目做到极致,就不要只用额外的辅助空间了! (不过使用Java刷题的录友,一定要使用辅助空间,因为Java里的string不能修改)
这么做有两个好处:
不用申请新数组。
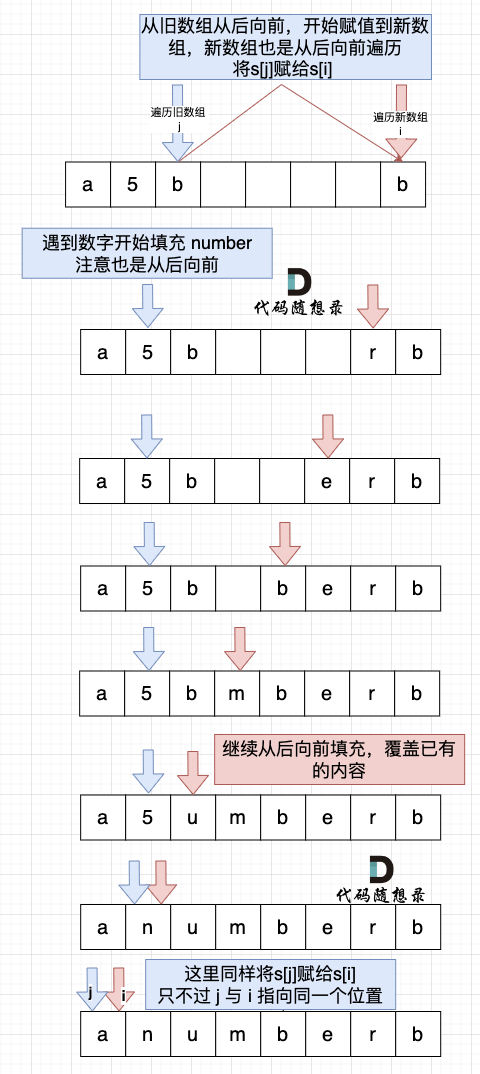
从后向前填充元素,避免了从前向后填充元素时,每次添加元素都要将添加元素之后的所有元素向后移动的问题。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 import java.util.Scanner;public class Main { public static String replaceNumber (String s) { int count = 0 ; int sOldSize = s.length(); for (int i = 0 ; i < s.length(); i++) { if (Character.isDigit(s.charAt(i))){ count++; } } char [] newS = new char [s.length() + count * 5 ]; int sNewSize = newS.length; System.arraycopy(s.toCharArray(), 0 , newS, 0 , sOldSize); for (int i = sNewSize - 1 , j = sOldSize - 1 ; j < i; j--, i--) { if (!Character.isDigit(newS[j])) { newS[i] = newS[j]; } else { newS[i] = 'r' ; newS[i - 1 ] = 'e' ; newS[i - 2 ] = 'b' ; newS[i - 3 ] = 'm' ; newS[i - 4 ] = 'u' ; newS[i - 5 ] = 'n' ; i -= 5 ; } } return new String (newS); }; public static void main (String[] args) { Scanner scanner = new Scanner (System.in); String s = scanner.next(); System.out.println(replaceNumber(s)); scanner.close(); } } import java.util.*;public class Main { public static void main (String[] args) { Scanner sc = new Scanner (System.in); String s = sc.next(); int len = s.length(); for (int i = 0 ; i < s.length(); i++) { if (s.charAt(i) >= 0 && s.charAt(i) <= '9' ) { len += 5 ; } } char [] ret = new char [len]; for (int i = 0 ; i < s.length(); i++) { ret[i] = s.charAt(i); } for (int i = s.length() - 1 , j = len - 1 ; i >= 0 ; i--) { if ('0' <= ret[i] && ret[i] <= '9' ) { ret[j--] = 'r' ; ret[j--] = 'e' ; ret[j--] = 'b' ; ret[j--] = 'm' ; ret[j--] = 'u' ; ret[j--] = 'n' ; } else { ret[j--] = ret[i]; } } System.out.println(ret); } }
151.翻转字符串里的单词 给你一个字符串 s ,请你反转字符串中 单词 的顺序。
示例 1:
示例 2:
想一下,我们将整个字符串都反转过来,那么单词的顺序指定是倒序了,只不过单词本身也倒序了,那么再把单词反转一下,单词不就正过来了。
所以解题思路如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 class Solution { public String reverseWords (String s) { StringBuilder sb = removeSpace(s); reverseString(sb, 0 , sb.length() - 1 ); reverseEachWord(sb); return sb.toString(); } private StringBuilder removeSpace (String s) { int start = 0 ; int end = s.length() - 1 ; while (s.charAt(start) == ' ' ) start++; while (s.charAt(end) == ' ' ) end--; StringBuilder sb = new StringBuilder (); while (start <= end){ char c = s.charAt(start); if (c != ' ' || sb.charAt(sb.length() - 1 ) != ' ' ){ sb.append(c); } start++; } return sb; } public void reverseString (StringBuilder sb, int start, int end) { while (start < end){ char temp = sb.charAt(start); sb.setCharAt(start, sb.charAt(end)); sb.setCharAt(end, temp); start++; end--; } } private void reverseEachWord (StringBuilder sb) { int start = 0 ; int end = 1 ; int n = sb.length(); while (start < n){ while (end < n && sb.charAt(end) != ' ' ){ end++; } reverseString(sb, start, end - 1 ); start = end + 1 ; end = start + 1 ; } } } class Solution { public String reverseWords (String s) { char [] initiaArr = s.toCharArray(); char [] newArr = new char [initiaArr.length + 1 ]; int newArrPos = 0 ; int i = initiaArr.length - 1 ; while (i >= 0 ){ while (i >= 0 && initiaArr[i] == ' ' ){i--;} int right = i; while (i>=0 && initiaArr[i] != ' ' ){i--;} for (int j = i+1 ; j <= right; j++){ newArr[newArrPos++] = initiaArr[j]; if (j == right){ newArr[newArrPos++] = ' ' ; } } } if (newArrPos == 0 ){ return "" ; }else { return new String (newArr, 0 , newArrPos-1 ); } } } class Solution { public String reverseWords (String s) { char [] initialArr = s.toCharArray(); reverse(initialArr, 0 , s.length() - 1 ); int k = 0 ; for (int i = 0 ; i < initialArr.length; i++) { if (initialArr[i] == ' ' ) { continue ; } int tempCur = i; while (i < initialArr.length && initialArr[i] != ' ' ) { i++; } for (int j = tempCur; j < i; j++) { if (j == tempCur) { reverse(initialArr, tempCur, i - 1 ); } initialArr[k++] = initialArr[j]; if (j == i - 1 ) { if (k < initialArr.length) { initialArr[k++] = ' ' ; } } } } if (k == 0 ) { return "" ; } else { return new String (initialArr, 0 , (k == initialArr.length) && (initialArr[k - 1 ] != ' ' ) ? k : k - 1 ); } } public void reverse (char [] chars, int begin, int end) { for (int i = begin, j = end; i < j; i++, j--) { chars[i] ^= chars[j]; chars[j] ^= chars[i]; chars[i] ^= chars[j]; } } } class Solution { public String reverseWords (String s) { char [] chars = s.toCharArray(); chars = removeExtraSpaces(chars); reverse(chars, 0 , chars.length - 1 ); reverseEachWord(chars); return new String (chars); } public char [] removeExtraSpaces(char [] chars) { int slow = 0 ; for (int fast = 0 ; fast < chars.length; fast++) { if (chars[fast] != ' ' ) { if (slow != 0 ) chars[slow++] = ' ' ; while (fast < chars.length && chars[fast] != ' ' ) chars[slow++] = chars[fast++]; } } char [] newChars = new char [slow]; System.arraycopy(chars, 0 , newChars, 0 , slow); return newChars; } public void reverse (char [] chars, int left, int right) { if (right >= chars.length) { System.out.println("set a wrong right" ); return ; } while (left < right) { chars[left] ^= chars[right]; chars[right] ^= chars[left]; chars[left] ^= chars[right]; left++; right--; } } public void reverseEachWord (char [] chars) { int start = 0 ; for (int end = 0 ; end <= chars.length; end++) { if (end == chars.length || chars[end] == ' ' ) { reverse(chars, start, end - 1 ); start = end + 1 ; } } } }
右旋字符串 字符串的右旋转操作是把字符串尾部的若干个字符转移到字符串的前面。给定一个字符串 s 和一个正整数 k,请编写一个函数,将字符串中的后面 k 个字符移到字符串的前面,实现字符串的右旋转操作。
输入示例
为了让本题更有意义,提升一下本题难度:不能申请额外空间,只能在本串上操作。 (Java不能在字符串上修改,所以使用java一定要开辟新空间)
其实两段反转就可以解决这个问题了
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 import java.util.Scanner;public class Main { public static void main (String[] args) { Scanner in = new Scanner (System.in); int n = Integer.parseInt(in.nextLine()); String s = in.nextLine(); int len = s.length(); char [] chars = s.toCharArray(); reverseString(chars, 0 , len - 1 ); reverseString(chars, 0 , n - 1 ); reverseString(chars, n, len - 1 ); System.out.println(chars); } public static void reverseString (char [] ch, int start, int end) { while (start < end) { ch[start] ^= ch[end]; ch[end] ^= ch[start]; ch[start] ^= ch[end]; start++; end--; } } } import java.util.Scanner;public class Main { public static void main (String[] args) { Scanner in = new Scanner (System.in); int n = Integer.parseInt(in.nextLine()); String s = in.nextLine(); int len = s.length(); char [] chars = s.toCharArray(); reverseString(chars, 0 , len - n - 1 ); reverseString(chars, len - n, len - 1 ); reverseString(chars, 0 , len - 1 ); System.out.println(chars); } public static void reverseString (char [] ch, int start, int end) { while (start < end) { ch[start] ^= ch[end]; ch[end] ^= ch[start]; ch[start] ^= ch[end]; start++; end--; } } }
28. 实现 strStr() 给你两个字符串 haystack 和 needle ,请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标(下标从 0 开始)。如果 needle 不是 haystack 的一部分,则返回 -1 。
示例 1:
示例 2:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 class Solution { public int strStr (String haystack, String needle) { int m = needle.length(); if (m == 0 ){ return 0 ; } int n = haystack.length(); if (n < m){ return -1 ; } int i = 0 ; int j = 0 ; while (i < n-m+1 ){ while (i < n && haystack.charAt(i) != needle.charAt(j)){ i++; } if (i == n){ return -1 ; } i++; j++; while (i < n && j < m && haystack.charAt(i) == needle.charAt(j)){ i++; j++; } if (j == m){ return i-j; }else { i -= j - 1 ; j = 0 ; } } return -1 ; } } class Solution { public void getNext (int [] next, String s) { int j = -1 ; next[0 ] = j; for (int i = 1 ; i < s.length(); i++){ while (j >= 0 && s.charAt(i) != s.charAt(j+1 )){ j = next[j]; } if (s.charAt(i) == s.charAt(j+1 )){ j++; } next[i] = j; } } public int strStr (String haystack, String needle) { if (needle.length() == 0 ){ return 0 ; } int [] next = new int [needle.length()]; getNext(next, needle); int j = -1 ; for (int i = 0 ; i < haystack.length(); i++){ while (j >= 0 && haystack.charAt(i) != needle.charAt(j+1 )){ j = next[j]; } if (haystack.charAt(i) == needle.charAt(j+1 )){ j++; } if (j == needle.length() - 1 ){ return (i-needle.length() + 1 ); } } return -1 ; } }
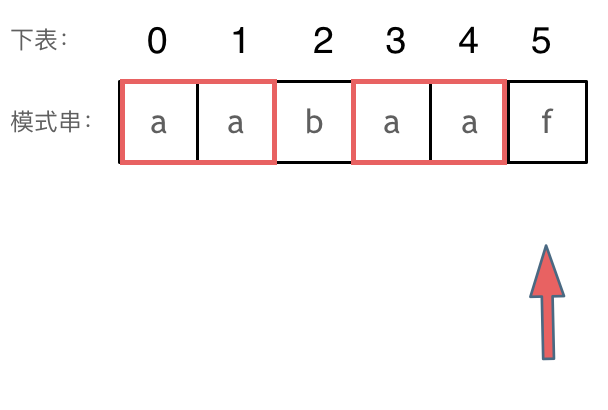
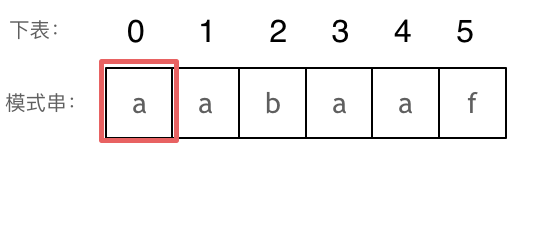
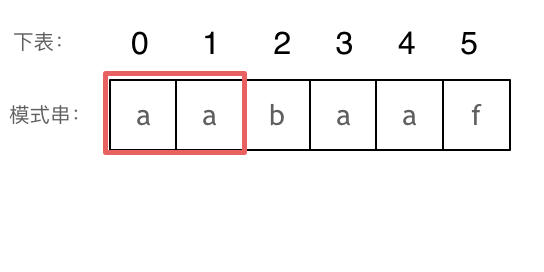
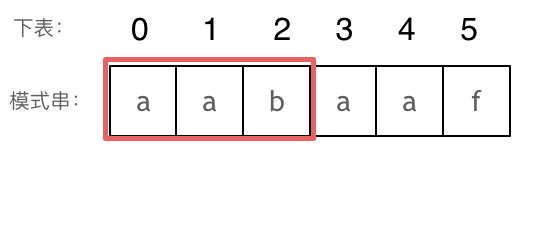
KMP算法 这道题其实核心算法是KMP算法,写过KMP的同学,一定都写过next数组,那么这个next数组究竟是个啥呢?next数组就是一个前缀表(prefix table)。
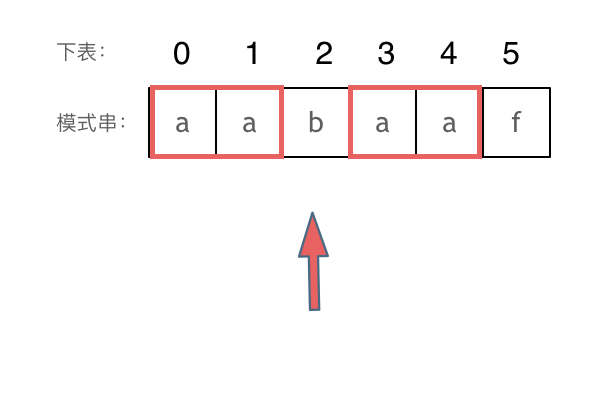
刚刚匹配的过程在下标5的地方遇到不匹配,模式串是指向f,如图:
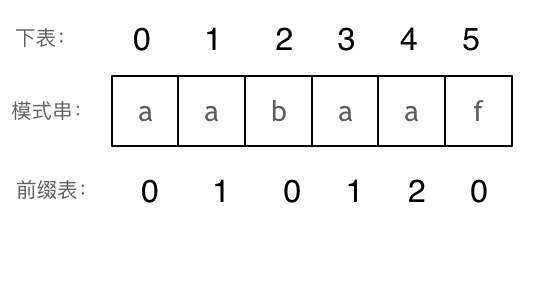
如何计算前缀表
前缀表与next数组
时间复杂度分析:其中n为文本串长度,m为模式串长度,因为在匹配的过程中,根据前缀表不断调整匹配的位置,可以看出匹配的过程是O(n),之前还要单独生成next数组,时间复杂度是O(m)。所以整个KMP算法的时间复杂度是O(n+m)的。
459.重复的子字符串 给定一个非空的字符串 s ,检查是否可以通过由它的一个子串重复多次构成。
示例 1:
示例 2:
示例 3:
暴力解法 暴力的解法, 就是一个for循环获取 子串的终止位置, 然后判断子串是否能重复构成字符串,又嵌套一个for循环,所以是O(n^2)的时间复杂度。只需要遍历到中间位置 ,因为子串结束位置大于中间位置的话,一定不能重复组成字符串。
结合KMP解法 假设我们有一个字符串 s = "abcabc",我们想要判断这个字符串是否由一个更短的子串通过重复组成的。
第一步:理解字符串重复的基本概念s 由重复的子串组成,比如 s = "abcabc" 可以看作是 "abc" 重复了两次。这就意味着,如果我们对 s 进行一定的操作,应该能够从中发现重复的模式。
第二步:构造新字符串s 复制并拼接自身,形成一个新的字符串 t = s + s,即 t = "abcabcabcabc"。
第三步:去除首尾字符t 的首尾字符,这样可以防止我们仅仅是在新字符串的开始或结束处找到原始的 s。去掉首尾字符后,t 变成 "bcabcabcab"。
第四步:搜索原始字符串t 中仍然能找到原始的字符串 s,这表明 s 确实是由重复的子串组成的。在我们的例子中,"abcabc" 确实出现在 "bcabcabcab" 中,从索引 1 到 6。
第五步:理解KMP算法的应用
第六步:代码实现和复杂度分析t.find(s) != std::string::npos 来实现,即检查 s 是否作为子串存在于 t 中。这种方法的时间复杂度通常为 O(n),空间复杂度为 O(1)。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 class Solution { public boolean repeatedSubstringPattern (String s) { if (s.equals("" )) return false ; int len = s.length(); s = " " + s; char [] chars = s.toCharArray(); int [] next = new int [len + 1 ]; for (int i = 2 , j = 0 ; i <= len; i++){ while (j > 0 && chars[i] != chars[j+1 ]) j = next[j]; if (chars[i] == chars[j + 1 ]) j++; next[i] = j; } if (next[len] > 0 && len % (len - next[len]) == 0 ){ return true ; } return false ; } }
字符串:总结篇 双指针法 在344.反转字符串 (opens new window),我们使用双指针法实现了反转字符串的操作,双指针法在数组,链表和字符串中很常用。
反转系列 在反转上还可以在加一些玩法,其实考察的是对代码的掌控能力。
KMP KMP的主要思想是当出现字符串不匹配时,可以知道一部分之前已经匹配的文本内容,可以利用这些信息避免从头再去做匹配了。
常见算法思路与实现
字符串反转 (344. 反转字符串)
使用双指针法来原地反转字符串,这种方法时间复杂度为 O(n),空间复杂度为 O(1)。
代码示例:1 2 3 4 5 6 7 8 public void reverseString (char [] s) { int left = 0 , right = s.length - 1 ; while (left < right) { char temp = s[left]; s[left++] = s[right]; s[right--] = temp; } }
局部字符串反转 (541. 反转字符串 II)
对特定的子串进行反转,可用于加密、文本处理等场景。
代码示例:1 2 3 4 5 6 7 8 9 10 11 12 public String reverseStr (String s, int k) { char [] a = s.toCharArray(); for (int start = 0 ; start < a.length; start += 2 * k) { int i = start, j = Math.min(start + k - 1 , a.length - 1 ); while (i < j) { char tmp = a[i]; a[i++] = a[j]; a[j--] = tmp; } } return new String (a); }
字符串中的单词翻转 (151. 翻转字符串里的单词)
先移除多余空格,再整体反转字符串,最后反转每个单词。
代码示例:1 2 3 4 5 6 public String reverseWords (String s) { s = s.trim(); String[] words = s.split("\\s+" ); Collections.reverse(Arrays.asList(words)); return String.join(" " , words); }
KMP算法 (28. 实现 strStr())
KMP 是用于字符串搜索的高效算法,通过计算“部分匹配”表来减少比较次数。
代码示例:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 public int strStr (String haystack, String needle) { if (needle.isEmpty()) return 0 ; int [] lps = computeLPSArray(needle); int i = 0 , j = 0 ; while (i < haystack.length()) { if (haystack.charAt(i) == needle.charAt(j)) { i++; j++; } if (j == needle.length()) { return i - j; } else if (i < haystack.length() && haystack.charAt(i) != needle.charAt(j)) { if (j != 0 ) j = lps[j - 1 ]; else i++; } } return -1 ; }
替换数字为字符串 (自定义题目)
针对字符串中的数字字符进行特定字符串的替换。
代码示例:1 2 3 4 5 6 7 8 public String replaceDigits (String s) { StringBuilder sb = new StringBuilder (); for (char c : s.toCharArray()) { if (Character.isDigit(c)) sb.append("number" ); else sb.append(c); } return sb.toString(); }