【算法】链表

g0dam

2024-09-11

Algorithm

链表

算法系列文章目前是跟着代码随想录学习

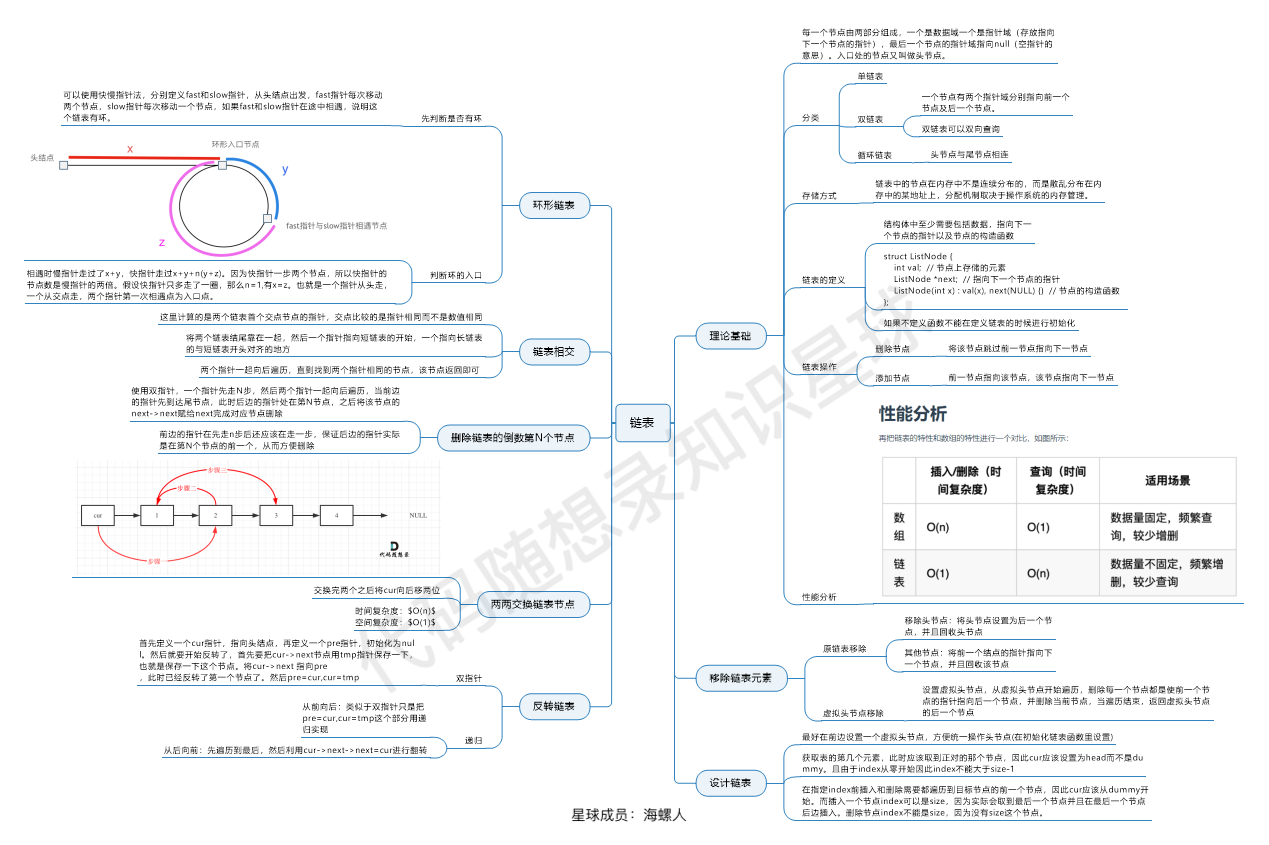
链表基础

单链表、双链表（每一个节点有两个指针域，一个指向下一个节点，一个指向上一个节点）、循环链表
链表操作的两种方式：直接使用原来的链表来进行操作。设置一个虚拟头结点在进行操作。
链表的存储方式：数组（内存中连续）、链表(内存中不连续)

链表类型：单链表、双链表、循环链表的基本构成和特点。
操作方式：直接修改原链表或使用虚拟头结点简化边界情况处理。
存储方式：链表通过非连续存储方式实现灵活的元素插入与删除。

链表操作与实现

设计链表 (707.设计链表)

实现一个链表类，包括添加、获取、删除节点的操作。

代码示例（单链表）:

class MyLinkedList {
    int size;
    ListNode head; // Sentinel node as pseudo-head

    public MyLinkedList() {
        size = 0;
        head = new ListNode(0);
    }

    // 实现方法省略...
}

代码示例（双链表）:

class MyLinkedList {
    int size;
    ListNode head, tail; // Sentinel nodes as pseudo-head and pseudo-tail

    public MyLinkedList() {
        size = 0;
        head = new ListNode(0);
        tail = new ListNode(0);
        head.next = tail;
        tail.prev = head;
    }

    // 实现方法省略...
}

反转链表 (206.反转链表)

使用迭代和递归方法实现链表反转。

代码示例（迭代方法）:

public ListNode reverseList(ListNode head) {
    ListNode prev = null, curr = head;
    while (curr != null) {
        ListNode nextTemp = curr.next;
        curr.next = prev;
        prev = curr;
        curr = nextTemp;
    }
    return prev;
}

代码示例（递归方法）:

public ListNode reverseList(ListNode head) {
    if (head == null || head.next == null) return head;
    ListNode p = reverseList(head.next);
    head.next.next = head;
    head.next = null;
    return p;
}

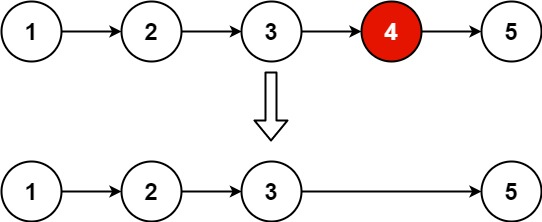
删除链表的倒数第 N 个结点 (19.删除链表的倒数第 N 个结点)

使用快慢指针技巧找到倒数第 N 个节点并删除。

代码示例:

public ListNode removeNthFromEnd(ListNode head, int n) {
    ListNode dummy = new ListNode(0);
    dummy.next = head;
    ListNode fast = dummy, slow = dummy;
    for (int i = 0; i <= n; i++) {
        fast = fast.next;
    }
    while (fast != null) {
        slow = slow.next;
        fast = fast.next;
    }
    slow.next = slow.next.next;
    return dummy.next;
}

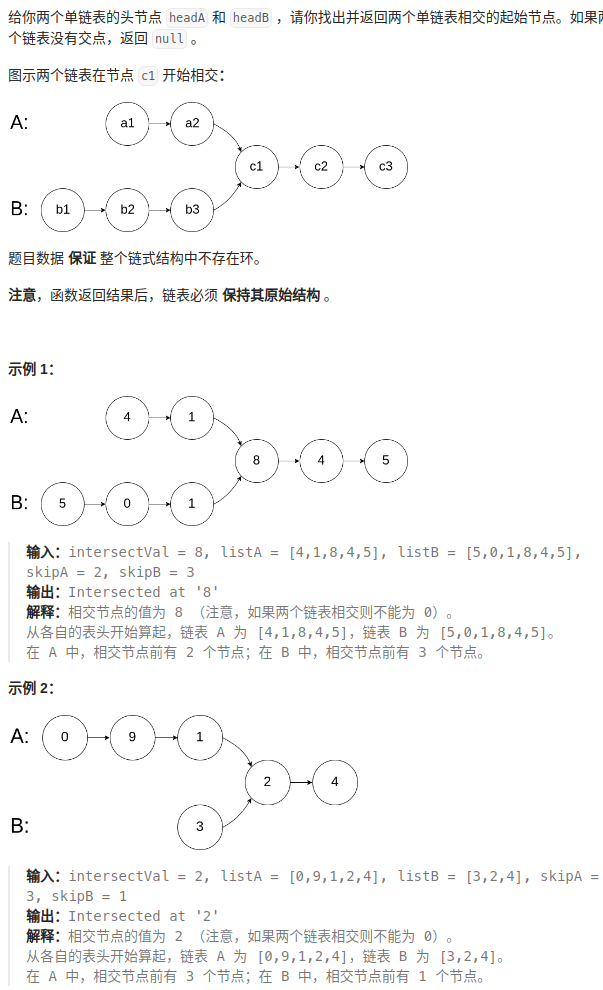
链表相交 (面试题 02.07.链表相交)

使用双指针策略检测并返回两个链表的相交点。

代码示例:

public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
    if (headA == null || headB == null) return null;
    ListNode a = headA, b = headB;
    while (a != b) {
        a = a == null ? headB : a.next;
        b = b == null ? headA : b.next;
    }
    return a;
}

环形链表 II (142.环形链表 II)

判断链表是否有环，并找到环的入口。

代码示例:

public ListNode detectCycle(ListNode head) {
    ListNode slow = head, fast = head;
    while (fast != null && fast.next != null) {
        slow = slow.next;
        fast = fast.next.next;
        if (slow == fast) {
            ListNode slow2 = head;
            while (slow2 != slow) {
                slow2 = slow2.next;
                slow = slow.next;
            }
            return slow;
        }
    }
    return null;
}

优化建议与高级技巧

虚拟头节点：使用虚拟头节点简化对链表头部节点的操作，尤其是在插入和删除操作中。
双指针技术：广泛应用于链表中，如在快速找到中点、倒数第 N 个节点、检测环等问题中。

707.设计链表

题意：
在链表类中实现这些功能：
get(index)：获取链表中第 index 个节点的值。如果索引无效，则返回-1。
addAtHead(val)：在链表的第一个元素之前添加一个值为 val 的节点。插入后，新节点将成为链表的第一个节点。
addAtTail(val)：将值为 val 的节点追加到链表的最后一个元素。
addAtIndex(index,val)：在链表中的第 index 个节点之前添加值为 val 的节点。如果 index 等于链表的长度，则该节点将附加到链表的末尾。如果 index 大于链表长度，则不会插入节点。如果index小于0，则在头部插入节点。
deleteAtIndex(index)：如果索引 index 有效，则删除链表中的第 index 个节点。

单链表版本

class ListNode{
    int val;
    ListNode next;
    ListNode(){}
    ListNode(int val){
        this.val = val;
    }
}

class MyLinkedList{
    int size;
    ListNode head;

    public MyLinkedList(){
        size = 0;
        head = new ListNode(0);
    }

    public int get(int index){
        if(index < 0 || index >= size) return -1;
        ListNode cur = head;
        for(int i = 0; i <= index; i++){
            cur = cur.next;
        }
        return cur.val;
    }

    public void addAtHead(int val){
        ListNode newNode = new ListNode(val);
        newNode.next = head.next;
        head.next = newNode;
        size++;
    }

    public void addAtTail(int val){
        ListNode newNode = new ListNode(val);
        ListNode cur = head;
        while(cur.next != null){
            cur = cur.next;
        }
        cur.next = newNode;
        size++;
    }

    public void addAtIndex(int index, int val){
        if(index > size){
            return;
        }
        if(index < 0){
            index = 0;
        }
        size++;
        ListNode pred = head;
        for(int i=0; i<index;i++){
            pred = pred.next;
        }
        ListNode toAdd = new ListNode(val);
        toAdd.next = pred.next;
        pred.next = toAdd;
    }

    public void deleteAtIndex(int index){
        if(index < 0 || index >= size){
            return;
        }
        size--;
        ListNode pred= head;
        for(int i = 0; i < index;i++){
            pred = pred.next;
        }
        pred.next = pred.next.next;
    }
}

双链表版本

class ListNode{
    int val;
    ListNode next,prev;
    ListNode(){}
    ListNode(int val){
        this.val = val;
    }
}

class MyLinkedList{
    int size;
    ListNode head,tail;

    public MyLinkedList(){
        size = 0;
        head = new ListNode(0);
        tail = new ListNode(0);
        head.next = tail;
        tail.prev = head;
    }

    public int get(int index){
        if(index < 0 || index >= size) return -1;
        ListNode cur = head;
        //判断哪边时间更短
        if(index >= size /2 ){
            cur = tail;
            for(int i = 0; i < size - index; i++){
                cur = cur.prev;
            }
        }else{
            for(int i = 0; i <= index; i++){
                cur = cur.next;
            }
        }
        return cur.val;
    }

    public void addAtHead(int val){
        addAtIndex(0, val);
    }

    public void addAtTail(int val){
       addAtIndex(size, val);
    }

    public void addAtIndex(int index, int val){
        if(index > size){
            return;
        }
        if(index < 0){
            index = 0;
        }
        size++;
        ListNode pred = head;
        for(int i=0; i<index;i++){
            pred = pred.next;
        }
        ListNode toAdd = new ListNode(val);
        toAdd.next = pred.next;
        pred.next.prev = toAdd;
        toAdd.prev = pred;
        pred.next = toAdd;
    }

    public void deleteAtIndex(int index){
        if(index < 0 || index >= size){
            return;
        }
        size--;
        ListNode pred= head;
        for(int i = 0; i < index;i++){
            pred = pred.next;
        }
        pred.next.next.prev = pred;
        pred.next = pred.next.next;
    }
}

206 反转链表

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。
// 双指针

class Solution {
    public ListNode reverseList(ListNode head) {
        if (head == null)  return null;
        ListNode prev = null;
        ListNode cur = head;
        ListNode tmp = null;
        while(cur != null){
            tmp = cur.next;
            cur.next = prev;
            prev = cur;
            cur = tmp;
        }
        return prev;
    }
}

// 递归

class Solution {
    public ListNode reverseList(ListNode head) {
        return reverse(null, head);
    }

    public ListNode reverse(ListNode prev, ListNode cur){
        if(cur == null) return prev;
        ListNode temp = null;
        temp = cur.next;
        cur.next = prev;
        return reverse(cur, temp);
    }
}

// 从后向前递归

class Solution {
    public ListNode reverseList(ListNode head) {
        // 边缘条件判断
        if(head == null) return null;
        if(head.next == null) return head;

        // 递归调用，翻转第二个节点开始往后的链表
        ListNode last = reverseList(head.next);
        // 翻转头结点与第二个节点的指向
        head.next.next = head;
        // 此时的head节点为尾节点，next需要指向null
        head.next = null;
        return last;
    }
}

// 使用虚节点的头插法

class Solution {
    public ListNode reverseList(ListNode head) {
        ListNode dummyHead = new ListNode(-1);
        dummyHead.next = null;
        ListNode cur = head;
        while(cur != null){
            ListNode temp = cur.next;
            // 头插法
            cur.next = dummyHead.next;
            dummyHead.next = cur;
            cur = temp;
        }
        return dummyHead.next;
    }
}

// 使用栈解决反转链表问题

class Solution {
    public ListNode reverseList(ListNode head) {
        if(head==null) return null;
        if(head.next == null) return null;

        Stack<ListNode> stack = new Stack<>();
        ListNode cur = head;
        while(cur != null){
            stack.push(cur);
            cur = cur.next;
        }

        ListNode pHead = new ListNode(0);
        cur = pHead;
        while(!stack.isEmpty()){
            ListNode node = stack.pop();
            cur.next = node;
            cur = cur.next;
        }

        cur.next = null;
        return pHead.next;
    }
}

这道题一开始没有让prev指向null出错了

24. 两两交换链表中的节点

给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。

class Solution {
    public ListNode swapPairs(ListNode head) {
        ListNode dumyhead = new ListNode(-1);
        dumyhead.next = head;
        ListNode cur = dumyhead;
        ListNode temp;
        ListNode firstnode;
        ListNode secondnode;
        while(cur.next != null && cur.next.next != null){
            temp = cur.next.next.next;
            firstnode = cur.next;
            secondnode = cur.next.next;
            cur.next = secondnode;
            secondnode.next = firstnode;
            firstnode.next = temp;
            cur = firstnode;
        }
        return dumyhead.next;
    }
}

// 递归解决

class Solution {
    public ListNode swapPairs(ListNode head) {
        if(head == null || head.next == null) return head;
        ListNode next = head.next;
        ListNode newNode = swapPairs(next.next);
        next.next = head;
        head.next = newNode;
        return next;
    }
}

19. 删除链表的倒数第 N 个结点

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

class Solution {
    public ListNode removeNthFromEnd(ListNode head, int n) {
        ListNode dummyhead = new ListNode(0);
        dummyhead.next = head;
        ListNode fast = dummyhead;
        ListNode slow = dummyhead;
        for(int i=0;i<n;i++){
            fast = fast.next;
        }
        while(fast.next != null){
            slow = slow.next;
            fast = fast.next;
        }
        if(slow.next == fast){
            fast = null;
        }else{
            slow.next = fast;   
        }
        return dummyhead.next;
    }
}

我上面的代码对于边界条件处理不好，下面是答案：
fast首先走n + 1步，为什么是n+1呢，因为只有这样同时移动的时候slow才能指向删除节点的上一个节点（方便做删除操作），如图：

class Solution {
    public ListNode removeNthFromEnd(ListNode head, int n) {
        ListNode dummyhead = new ListNode(0);
        dummyhead.next = head;
        ListNode fast = dummyhead;
        ListNode slow = dummyhead;
        for(int i=0;i<=n;i++){
            fast = fast.next;
        }
        while(fast != null){
            slow = slow.next;
            fast = fast.next;
        }
        // 此时 slowIndex 的位置就是待删除元素的前一个位置。
        // 具体情况可自己画一个链表长度为 3 的图来模拟代码来理解
        // 检查 slowIndex.next 是否为 null，以避免空指针异常
        if(slow.next != null){
            slow.next = slow.next.next;
        }
        return dummyhead.next;
    }
}

我又自己写了个，按照我原来的思路：

class Solution {
    public ListNode removeNthFromEnd(ListNode head, int n) {
        ListNode dummyhead = new ListNode(0);
        dummyhead.next = head;
        ListNode fast = dummyhead;
        ListNode slow = dummyhead;
        for(int i=0;i<n;i++){
            fast = fast.next;
        }
        while(fast.next != null){
            slow = slow.next;
            fast = fast.next;
        }
        // 此时 slowIndex 的位置就是待删除元素的前一个位置。
        // 具体情况可自己画一个链表长度为 3 的图来模拟代码来理解
        // 检查 slowIndex.next 是否为 null，以避免空指针异常
        slow.next = slow.next.next;
        return dummyhead.next;
    }
}

面试题 02.07. 链表相交

思路是先让链表指针移动到剩余长度相同的位置，然后让两个链表同时移动，直到遇到相同的节点，或者遇到null。注意这道题相交节点处指针是相同的，我开始还在想还要对比后面的节点。

public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        ListNode curA = headA;
        ListNode curB = headB;
        int lenA = 0, lenB = 0;
        while(curA != null){
            lenA++;
            curA = curA.next;
        }

        while(curB != null){
            lenB++;
            curB = curB.next;
        }
        curA = headA;
        curB = headB;
        if(lenB > lenA){
            int tmpLen = lenA;
            lenA = lenB;
            lenB = tmpLen;
            ListNode tmpNode = curA;
            curA = curB;
            curB = tmpNode;
        }
        // 求长度差
        int gap = lenA - lenB;
        // 让curA和curB在同一起点上
        while(gap-- > 0){
            curA = curA.next;
        }
        while(curA != null){
            if(curA == curB){
                return curA;
            }
            curA = curA.next;
            curB = curB.next;
        }
        return null;
    }
}

下面的版本是同步走的版本：

 //合并链表同步移动
public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
       // p1指向A链表头节点，p2指向B链表头节点
       ListNode p1 = headA, p2 = headB;
       while(p1 != p2){
        // p1走一步，如果走到A链表末尾，转到B链表
        if(p1 == null) p1 = headB;
        else p1 = p1.next;
        // p2走一步，如果走到B链表末尾，转到A链表
        if(p2 == null) p2 = headA;
        else p2 = p2.next;
       }
       return p1;
    }
}

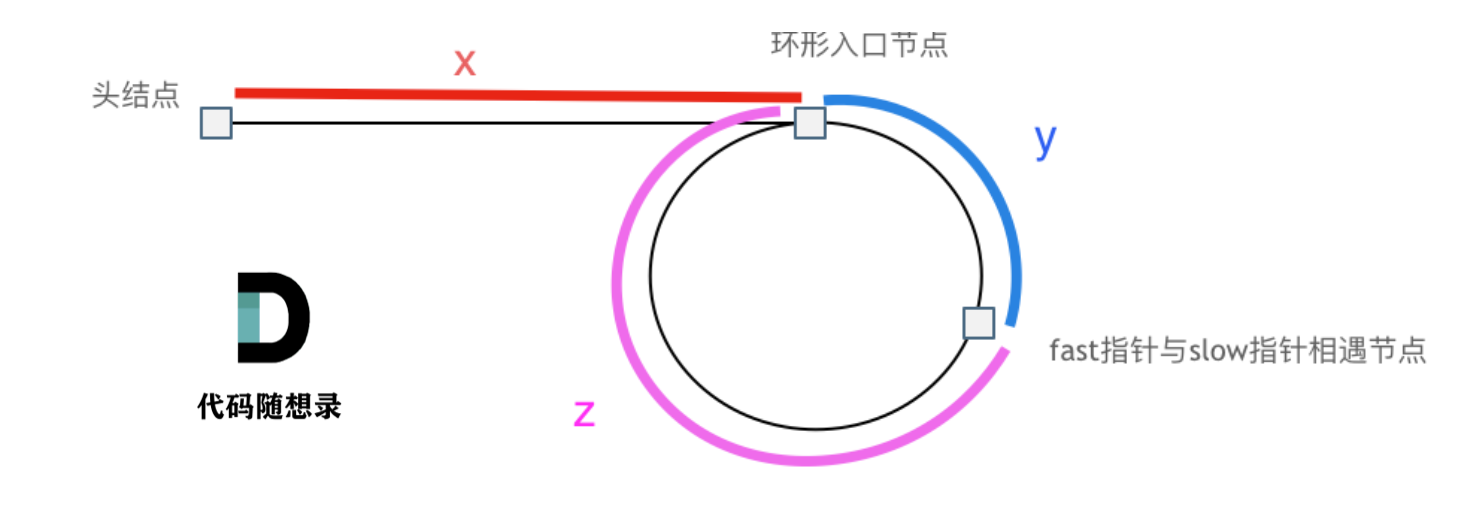
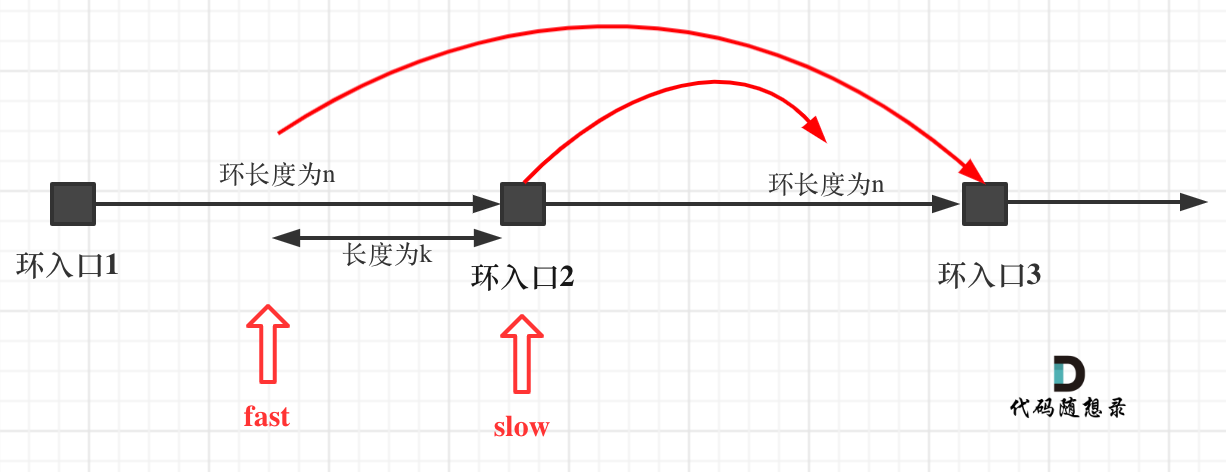
142.环形链表II

判断链表是否有环
可以使用快慢指针法，分别定义 fast 和 slow 指针，从头结点出发，fast指针每次移动两个节点，slow指针每次移动一个节点，如果 fast 和 slow指针在途中相遇，说明这个链表有环。
为什么fast 走两个节点，slow走一个节点，有环的话，一定会在环内相遇呢，而不是永远的错开呢
首先第一点：fast指针一定先进入环中，如果fast指针和slow指针相遇的话，一定是在环中相遇，这是毋庸置疑的。
那么来看一下，为什么fast指针和slow指针一定会相遇呢？
可以画一个环，然后让 fast指针在任意一个节点开始追赶slow指针。这是因为fast是走两步，slow是走一步，其实相对于slow来说，fast是一个节点一个节点的靠近slow的，所以fast一定可以和slow重合。

如果有环，如何找到这个环的入口
此时已经可以判断链表是否有环了，那么接下来要找这个环的入口了。
假设从头结点到环形入口节点的节点数为x。环形入口节点到 fast指针与slow指针相遇节点节点数为y。从相遇节点再到环形入口节点节点数为 z。
那么相遇时： slow指针走过的节点数为: x + y， fast指针走过的节点数：x + y + n (y + z)，n为fast指针在环内走了n圈才遇到slow指针，（y+z）为一圈内节点的个数A。

因为fast指针是一步走两个节点，slow指针一步走一个节点，所以 fast指针走过的节点数 = slow指针走过的节点数 * 2：
(x + y) * 2 = x + y + n (y + z)
两边消掉一个（x+y）: x + y = n (y + z)
因为要找环形的入口，那么要求的是x，因为x表示头结点到环形入口节点的的距离。
所以要求x ，将x单独放在左面：x = n (y + z) - y ,
再从n(y+z)中提出一个（y+z）来，整理公式之后为如下公式：x = (n - 1) (y + z) + z 注意这里n一定是大于等于1的，因为 fast指针至少要多走一圈才能相遇slow指针。
这个公式说明什么呢？
先拿n为1的情况来举例，意味着fast指针在环形里转了一圈之后，就遇到了 slow指针了。
当 n为1的时候，公式就化解为 x = z，
这就意味着，从头结点出发一个指针，从相遇节点也出发一个指针，这两个指针每次只走一个节点，那么当这两个指针相遇的时候就是环形入口的节点。
也就是在相遇节点处，定义一个指针index1，在头结点处定一个指针index2。
让index1和index2同时移动，每次移动一个节点，那么他们相遇的地方就是环形入口的节点。

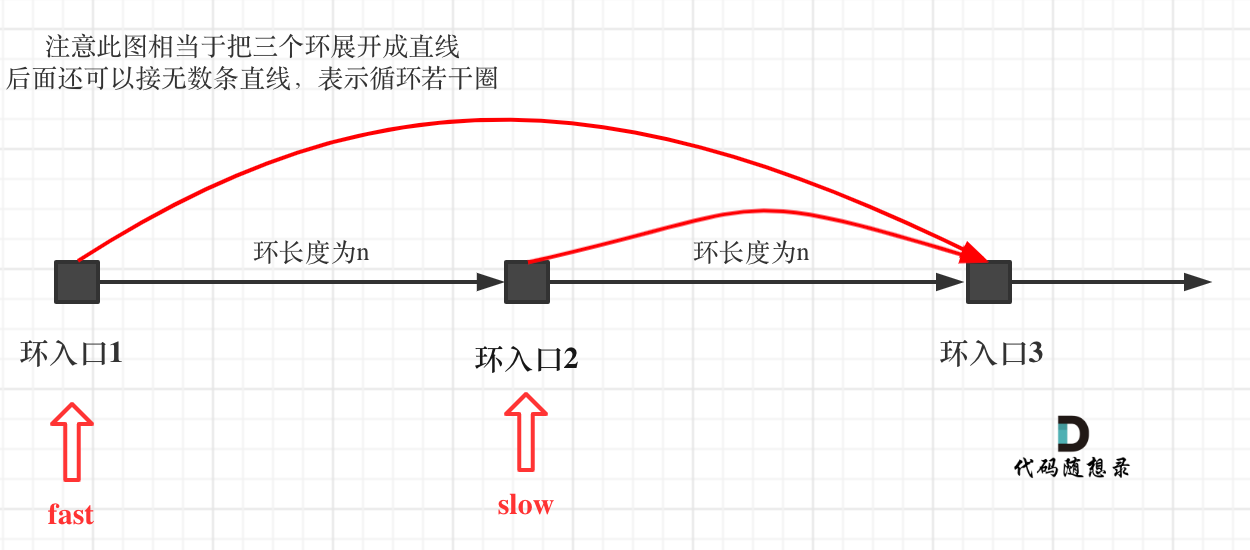
那么 n如果大于1是什么情况呢，就是fast指针在环形转n圈之后才遇到 slow指针。
其实这种情况和n为1的时候效果是一样的，一样可以通过这个方法找到环形的入口节点，只不过，index1 指针在环里多转了(n-1)圈，然后再遇到index2，相遇点依然是环形的入口节点。

在推理过程中，大家可能有一个疑问就是：为什么第一次在环中相遇，slow的步数是 x+y 而不是 x + 若干环的长度 + y 呢？
首先slow进环的时候，fast一定是先进环来了。
如果slow进环入口，fast也在环入口，那么把这个环展开成直线，就是如下图的样子：

可以看出如果slow 和 fast同时在环入口开始走，一定会在环入口3相遇，slow走了一圈，fast走了两圈。
重点来了，slow进环的时候，fast一定是在环的任意一个位置，如图：

那么fast指针走到环入口3的时候，已经走了k + n 个节点，slow相应的应该走了(k + n) / 2 个节点。
因为k是小于n的（图中可以看出），所以(k + n) / 2 一定小于n。
也就是说slow一定没有走到环入口3，而fast已经到环入口3了。
这说明什么呢？
在slow开始走的那一环已经和fast相遇了。
那有同学又说了，为什么fast不能跳过去呢？在刚刚已经说过一次了，fast相对于slow是一次移动一个节点，所以不可能跳过去。

public class Solution {
    public ListNode detectCycle(ListNode head) {
        ListNode slow = head;
        ListNode fast = head;
        while(fast != null && fast.next != null){
            slow = slow.next;
            fast = fast.next.next;
            if(slow == fast){
                ListNode index1 = fast;
                ListNode index2 = head;
                while(index1 != index2){
                    index1 = index1.next;
                    index2 = index2.next;
                }
                return index1;
            }
        }
        return null;
    }
}


// 利用哈希表实现 非常直观的思路是：我们遍历链表中的每个节点，并将它记录下来；一旦遇到了此前遍历过的节点，就可以判定链表中存在环。时间空间复杂度都是O(N)
public class Solution {
    public ListNode detectCycle(ListNode head) {
        ListNode pos = head;
        Set<ListNode> visited = new HashSet<ListNode>();
        while(pos != null){
            if(visited.contains(pos)){
                return pos;
            }else{
                visited.add(pos);
            }
            pos = pos.next;
        }
        return null;
    }
}